The philosophy of modeling
Modeling is a mental activity that lets us think and prepare models to describe how different objects, people, and devices behave. These models are then used to extract more complex information A model is a translation of an idea or a phenomenon into a form that makes it easy to understand. For example, in schools, teachers show a dummy skeleton of the human body to teach human anatomy. With the skeleton as a model, it becomes easier to locate ribs, girdles, and other body parts that are otherwise hidden in the world behind our skin. The plastic model for the human respiratory system, the Watermelon analogy of Thomson’s atoms, nucleus as a liquid drop, all these are beautiful examples of human efforts towards simplifying the complex problems.
What is mathematics?
- Mathematics is an exact and precise language of nature. This helps us to formulate our beliefs and ideas and prove the assumptions. It acts as a cement between our beliefs or ideas and real phenomena.
- Mathematics is a succinct language with well-defined rules for manipulation.
- Mathematics is the science that deals with the logic of shape, quantity, and qualitative arrangements.
- Pure mathematicians prove theorems and applied mathematics construct theories.
- The idea of applied math create methods that solve problems in science. Modern areas of applied math include mathematical physics, mathematical biology, and math finance.
- The normal methodology in applied mathematical science is to fabricate a scientific model of genuine wonder, fathom model, and create suggestions for execution improvement.
Mathematical Modelling
A mathematical model is a way of presenting the experimental results and natural phenomena in mathematical language to describe the behavior of the system. It is widely used in natural science and engineering disciplines (physics, chemistry, biology, and all engineering) and also in social development sciences such as sociology, environmental science, and economics. It has many advantages to present proof of real phenomena.
Now lets come to our motto of mathematical modeling. The process of developing a model using tools in mathematics is mathematical modeling To make a mathematical model we have to go a certain procedure that makes our model correct.

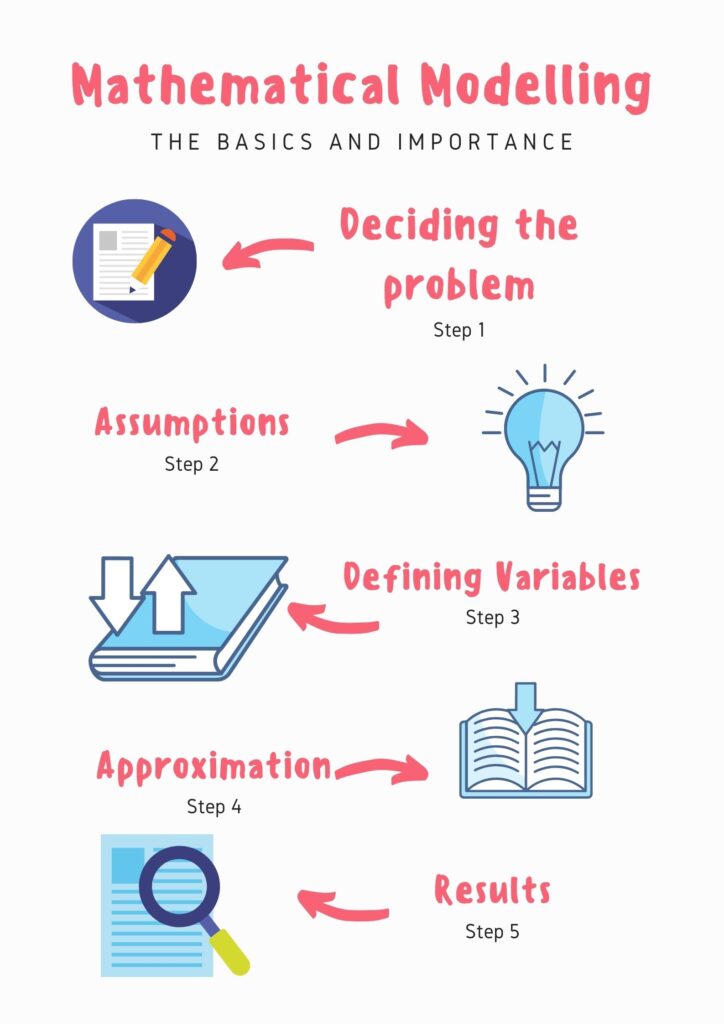
The following procedure we have to follow to make a precise and feasible mathematical model
1. Deciding the problem
The main task to build any mathematical model is to decide your problem. Problem is a tough task because if decide your problem you are almost cover 30% of the mathematical modeling journey. So carefully note down the main key factors that you have to focus on.
Go through the brief literature
First of all, you know all about the phenomena or experiments. Point out some important details about observations. Try to find any findings that have been reported before you. Compiling all together and think about your observations.
Find what you want to know
After the literature survey, now you have to decide what you won’t know. That means you want to know some small details about your observations. Those small details lead to your problem.
Already what you know
Try to point out that what you know about your observations from your past study experience and recent literature survey. Because it plays an important in deciding the problem.
after doing all three steps. Collects all knowledge you got from the above three steps in one place. And now deciding a problem is a little bit easy. Because without these three steps you will lend at a different place. Let say you have decided your without following these steps, you will in your middle journey that this is not feasible or already done. So go step by step.
2. Make assumptions
After deciding your problem, the next important step is making the assumption for your model. Because in nature things are ideal but in our experiments, things are not ideal. So to see your model in a feasible world you have to make assumptions that depict your model in a certain boundary. Because to view and to analyze ideal things, the ideal functions required. Mathematics is a precise language. but ideal? I doubt.
3. Defining the variables
After deciding the problems and making the assumption the next important step is pointing out the variables that vary in the model and give some results with variations. Those variables lead to the phenomena that observe during experiments.
4. Making Approximations
And approximation is the boundary up to which the variables can vary. Because boundary is necessary to see your phenomena again by modeling. Approximation for the variables is important.
5. Results and Analysis
After doing all the steps pointed above, the next step is to perform on your mathematical equations. You can get results by solving those mathematical equations by Numerically and Analytically. And try to analyses your results with your experimental results.
No Responses